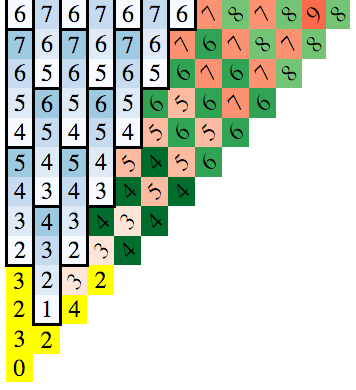
First time I faced this problem during one of my codility tests for a work application. And I failed it. :) Just because I have never heard about such problems before. Anyway, my opinion about codility tests is the same as about writing code on a whiteboard. A programmer should be able to think, to investigate and solve the problem in the end. You can’t train yourself for every existing problem and their endless variations. It’s true especially for whiteboard coding challenge because you have limited time and can’t use online resources. Stress not compliment process of thinking, it destroys this process. Well, it’s a topic for another post. In this post, I will provide my investigation on a Knight distance problem and a solution.
I’m a kind of person who likes to accomplish things. And that’s why I did this investigation later after my test. I will give material step by step as I found it and realized new things.
The Knight distance problem could be described as a problem to find a count of moves which Knight needs to reach a point on a chess board. In our case chess board will be infinite.
The first link which I found was this GitHub repo with a very explanatory readme and even sketches.
https://github.com/Jarosh/Exercises/wiki/Finding-the-shortest-path-as-for-knight–in-the-game-of-chess-on-an-infinite-board
Because of confidence of an author I used this approach for my test. And now I know that this solution is totally wrong. It’s because an author supposed, that Knight can’t move backward, only forward. In this case, his solution is correct. But in the task wasn’t mentioned any restriction on Knight moves directions. This assumption leads to wrong task interpretations. Some GitHub users, as I am, already left an issue in this repo with their thoughts about a wrong solution. Anyway, I will provide a code.
The most pity about that solution is a fact, that I have found the best possible solution during the test and had both on hands. But because of wrong solution confident explanation from an author, I have chosen his version. And only now I have realized how this decision impacts on my life now…
NEXT TWO SOLUTIONS ARE WRONG. BECAUSE OF NO BACKWARD MOVE ASSUMPTION.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
function solution($A, $B) { // write your code in PHP7.0 $limit = 100000000; if (abs($A) > $limit || abs($B) > $limit) { return -1; } $checkBoundaries = ($A / $B >= 0.5 && $A / $B <= 2) || ($A / $B <= -0.5 && $A / $B >= -2); $checkReachable = ($A + $B) % 3 == 0; if (($checkBoundaries) && ($checkReachable)) { $turns = ($A + $B) / 3; if ($turns > $limit) { //it's hard to get -2 return -2; } return $turns; } else { return -1; } } |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
function solution3($A, $B) { $limit = 100000000; if (abs($A) > $limit || abs($B) > $limit) { return -1; } $dx = abs($A); $dy = abs($B); $moves = max(floor(($dx + 1) / 2), floor(($dy + 1) / 2), floor(($dx + $dy + 2) / 3)); while (($moves % 2) != ($dx + $dy) % 2 && $moves <= $limit) { $moves++; } return $moves <= $limit ? $moves : -2; } |
And the test code for these “solutions”.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
echo '---first---' . PHP_EOL; print_r(solution(4, 5)); echo PHP_EOL; //print_r(solution(1, 0)); echo PHP_EOL; print_r(solution(2, 2)); echo PHP_EOL; print_r(solution(4, 4)); echo PHP_EOL; |
|
1 2 3 4 5 6 7 8 9 10 11 12 |
echo '---third---' . PHP_EOL; print_r(solution3(4, 5)); echo PHP_EOL; print_r(solution3(1, 0)); echo PHP_EOL; print_r(solution3(2, 2)); echo PHP_EOL; print_r(solution3(4, 4)); echo PHP_EOL; |
Well, let’s move to something that really works correctly. But too slow.
Next thing which I have tried of course was a recursion. The idea is simple: we need to go deep and found and answer somewhere on the bottom. As a basis, I have used javascript code from this gist.
https://gist.github.com/adamloving/6a4c563b75110c1fade0
The problem here is a performance. Especially with PHP. Javascript is a language which all about functions and callbacks. And it’s optimized for a lot of functions calls. PHP isn’t. Even an author of this gist mentioned, that solution fast at depth 100 and became slow on 1000 depth. In PHP (version 7) this function can’t go deeper than 5 depth with adequate response time. :)
Anyway, I have translated the code into PHP code and will publish it.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 |
//works with recursion but slow in php function solution4($A, $B) { return countMovesTo(["x" => $A, "y" => $B]); } function countMovesTo(array $destination, $depth = 0, $cache = []) { $limit = 100000000; if (abs($destination['x']) > $limit || abs($destination['y']) > $limit) { return -1; } $depth = $depth ?? 0; $cache = $cache ?? []; $cachedR = $cache[$destination["x"]] ?? []; $result = $cachedR[$destination["y"]] ?? []; if ($result) { return $result; } if ($destination["x"] == 0 && $destination["y"] == 0) { $result = 0; } else if ($depth > 5) { $result = -2; } else { $minMoves = $limit; $nextPositions = getNextPositions($destination); for ($i = 0; $i < count($nextPositions); $i++) { $nextPosition = $nextPositions[$i]; $result = countMovesTo($nextPosition, $depth + 1, $cache); if ($result < 0) { continue; } $minMoves = min($minMoves, 1 + $result); } if ($minMoves >= $limit) { $result = -2; } else { $result = $minMoves; } } $cache[$destination["x"]] = $cache[$destination["x"]] ?? []; $cache[$destination["x"]][$destination["y"]] = $result; return $result; } function getNextPositions($start) { $moves = [ ["x" => -2, "y" => -1], ["x" => -2, "y" => +1], ["x" => -1, "y" => -2], ["x" => -1, "y" => +2], ["x" => +1, "y" => -2], ["x" => +1, "y" => +2], ["x" => +2, "y" => -1], ["x" => +2, "y" => +1] ]; $positions = []; for ($i = 0; $i < count($moves); $i++) { $move = $moves[$i]; $position = []; $position["x"] = $start["x"] + $move["x"]; $position["y"] = $start["y"] + $move["y"]; $positions[] = $position; } return $positions; } echo '---fourth---' . PHP_EOL; print_r(solution4(4, 5)); echo PHP_EOL; print_r(solution4(1, 0)); echo PHP_EOL; print_r(solution4(2, 2)); echo PHP_EOL; print_r(solution4(4, 4)); echo PHP_EOL; print_r(solution4(9, 9)); echo PHP_EOL; |
And now the best question which could be asked – how we could do the same, but better? The answer as simple as Dijkstra algorithm and a BFS one.
Introducing BFS algorithm.
I haven’t tried Dijkstra but was very interested in BFS. First of all, I want to mention that I have never touched such algorithms before. Maybe only in University, but I don’t remember anything. So, I found BFS description. Then I found simple implementation with PHP in this git repository.
https://github.com/lextoumbourou/bfs-php
And, actually, I found a solution based on C++ and BFS.
http://www.techiedelight.com/chess-knight-problem-find-shortest-path-source-destination/
The problem here is the same as with recursion. Probably BFS could help to search deeply when it runs with C++, but not with PHP. PHP implementation became slow from positions like 7,7 and 8,8. It’s easy could be explained because of nature of BFS algorithm. As deeper we go, as many function calls, we have. It’s like a tree with all possible variants which we should call an check.
The code of BFS solution with PHP is here.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
//works but slow search function solution6($A, $B) { return bfsKnight(new Node(0, 0), new Node($A, $B)); } /** * example ! * @param $graph * @param $start * @param $end * @return bool */ function bfs($graph, $start, $end) { $queue = new SplQueue(); $queue->enqueue($start); $visited = [$start]; while ($queue->count() > 0) { $node = $queue->dequeue(); # We've found what we want if ($node === $end) { return true; } foreach ($graph[$node] as $neighbour) { if (!in_array($neighbour, $visited)) { # Mark neighbour visited $visited[] = $neighbour; # Enqueue node $queue->enqueue($neighbour); } }; } return false; } echo '---sixth---' . PHP_EOL; print_r(solution6(4, 5)); echo PHP_EOL; print_r(solution6(1, 0)); echo PHP_EOL; print_r(solution6(2, 2)); echo PHP_EOL; print_r(solution6(4, 4)); echo PHP_EOL; print_r(solution6(7, 7)); echo PHP_EOL; |
Looks great. But useless with PHP.
And the winner is …
An analytical function!
http://stackoverflow.com/questions/2339101/knights-shortest-path-chess-question/41704071#41704071
As I mentioned above I had the link to StackOverflow answer from the beginning. Just lack of experience and knowledge about such problems led me to choose a different solution (and also a confidence of an author of the wrong solution). In answers to this question was mentioned Dijkstra algorithm and a BFS. But I have recognized it’s later.
But the fastest solution with O(1) complexity is an analytical function which was proposed as a solution on SACO 2007 Day 1. It’s really fast and based on a formula described here.
The PHP code for this one is:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 |
//works and fastest //0 <= y <= x function solution2($A, $B) { $limit = 100000000; if (abs($A) > $limit || abs($B) > $limit) { return -1; } // axes symmetry $A = abs($A); $B = abs($B); // diagonal symmetry if ($A < $B) { $t = $A; $A = $B; $B = $t; } // 2 corner cases if ($A == 1 && $B == 0) { return 3; } if ($A == 2 && $B == 2) { return 4; } $delta = $A - $B; // if ($B > $delta) // return 2 * (($B - $delta) / 3) + $delta; // else // return $delta - 2 * (($delta - $B) / 4); if ($B > $delta) { return $delta - 2 * floor(($delta - $B) / 3); } else { return $delta - 2 * floor(($delta - $B) / 4); } } echo '---second---' . PHP_EOL; print_r(solution2(4, 5)); echo PHP_EOL; print_r(solution2(1, 0)); echo PHP_EOL; print_r(solution2(2, 2)); echo PHP_EOL; print_r(solution2(4, 4)); echo PHP_EOL; print_r(solution2(9, 9)); echo PHP_EOL; print_r(solution2(20, 20)); echo PHP_EOL; print_r(solution2(1, 1)); echo PHP_EOL; |
A commented out version is a wrong interpretation of a formula.
And yes, it works for 20,20 or for any point on an infinite board in just ms. The base assumptions here to get this formula are:
– x and y are symmetrical.
– we could convert all x,y in symmetrical one
– then we could use delta = x – y in a formula and all that we need consider is a position of y relative to this delta. so we have two possible cases when y is bigger or less the delta.
In the end, it’s easy to get into this formula. It requires just analytical skills and good math basis.
That’s it!
And again I want to put stress again on a fact, that sharing bad, not working or not researched to the end solutions is a very bad idea. Such solution when published could make a great impact on somebody life. It will not help, but otherwise, it could harm somebody career and change life decisions. In my case, it was a decision to work remotely or relocate to another country from Russia. And because I failed the test with a wrong solution I haven’t other options that start looking for a relocation job. And I have found it.
If I would send the second one solution, which is right and fastest, that probably I would continue work remotely. It’s a life, any small thing could have a huge influence of how and in which direction it would go. We just can’t, haven’t time and resources, to check all possible variants as in BFS algorithm.